Course Overview: Applications
Overview
We have to review some core tools/ideas in statistics:
- Basics of distributions, populations vs sample. Mean, variance, etc
- Sample mean \(\rightarrow\) large sample theory \(\rightarrow\) population mean (estimation)
- Hypothesis testing and confidence intervals
- Linear models and linear regression
First, some research to motivate us.
Application 1: Credit Constraints and Human Capital
- “The Nature of Credit Constraints and Human Capital”, Lochner and Monge-Naranjo, American Economic Review (2011)
- Theory:
- Incomplete markets can lead to underinvestment in human capital (agents cannot borrow against returns to investment).
- Controlling for returns, income/wealth should not predict investment unless borrowing constraints bind.
- Question: Evidence of credit constraints in college enrollment decisions?
- Data NLSY79 and NLSY 97 (two cohorts of young individuals)
- Key idea: How do skills (measured by AFQT) and parental income predict college enrollment?
Application 1: Credit Constraints and Human Capital
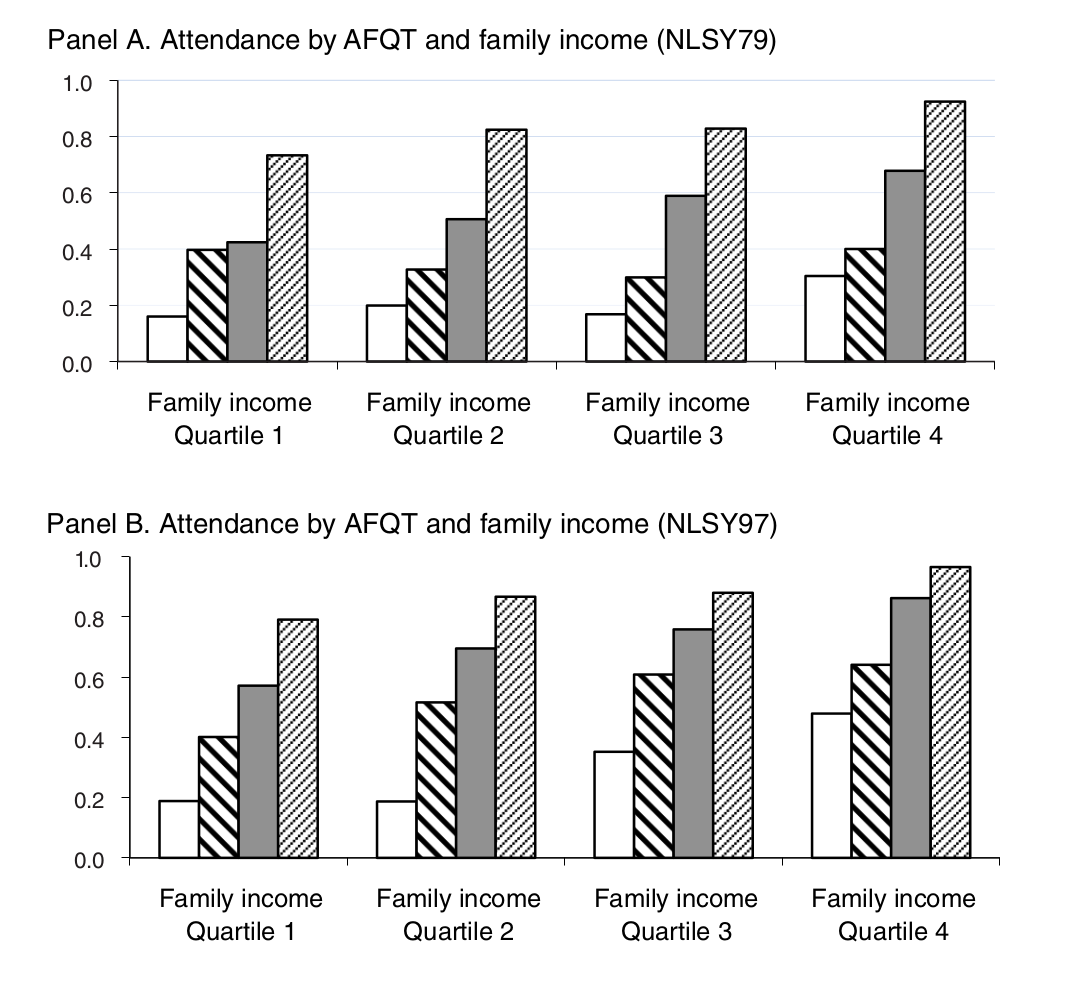
- Consistent gradient in AFQT (cog skill)
- Family income more important in 97 cohort
- Suggestive evidence of more binding constraints
- No testing here: how to test formally?
Application 2: Teacher Incentives in Rural India
- Paper: “Incentives Work: Getting Teachers to Come to School”, Duflo, Hanna, and Ryan, American Economic Review (2012)
- Background: expanding access to primary education crucial in developing countries. Teacher absenteeism in India is a big problem.
- Theory: providing incentives should increase attendance.
- The Paper: evaluates a teacher incentive program by RCT.
- Data: Attendance and student outcomes for 57 treatment schools, 56 control schools run by Seva Mandir (NGO)
Application 2: Teacher Incentives in Rural India
Details on “treatment”:
- Monitoring via tamper-proof cameras.
- Financial incentives for teachers: \[ \text{Rupees per month} = 500 + 50\times\max\{0,D - 10\} \] where \(D\) is days attended per month.
- Financial incentives or fear of punishment?
- Notice: no incentive if: \[ \text{Days attended so far} + \text{Days left in month} \leq 10 \]
Application 2: Teacher Incentives in Rural India
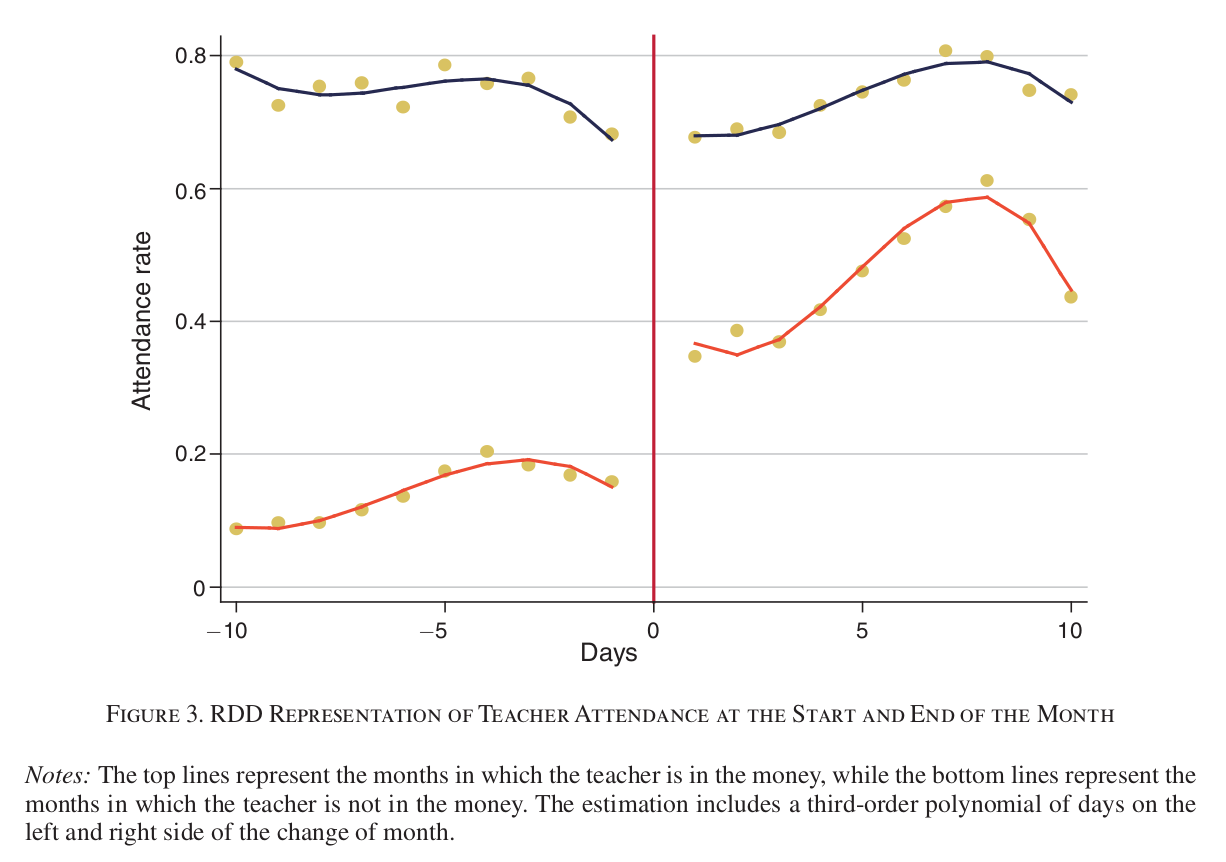
- Visual evidence of effect.
- But how to estimate size of effect?
- Quantify uncertainty?
- No testing here: how to test formally?
- Can do a regression analysis…
Application 2: Teacher Incentives in Rural India
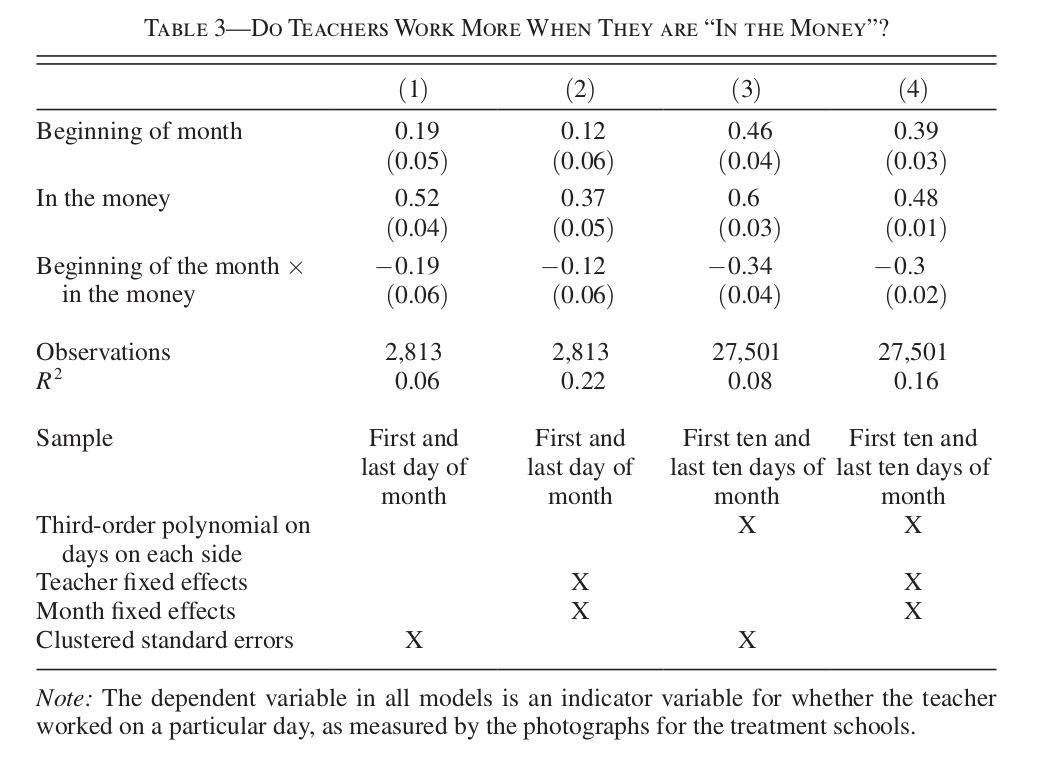
- How to interpret this table?
- How are standard errors calculated? \(R^2\)?
- Fixed Effects? Clustering?
- Will learn how to replicate and interpret this graph.